Advocacy
Dojo (HowTo)
Reference
Markets
Museum
News
Other
![]()
Myths
Press
General
Hack
Hardware
Interface
Software
Standards
People
Forensics
Web
CodeNames
Easter Eggs
History
Innovation
Sightings
Opinion
Martial Arts
ITIL
Thought

![]()
|
A question that I get surprisingly often is "why are computers binary / digital?" -- or variations on that theme. Having only on/off only (zero or one) is binary, and having many levels or degrees is analog. So it seems logical that if you have only two levels ("on" and "off"), then having more levels (like 4, 10 or 100 levels) would mean that the computer could do more in the same amount of time. So why shouldn't computers be analog? Well there have been a few analog computers and devices but for the most part what sounds logical may not be (in electronics) when you know more about the problem. Let me explain why.
Remember, this is just a high level explanation meant to give people a basic understanding of the concepts - all these issues are more complex than explained, but at least this will give people the right idea.
Analog and Digital
Imagine the signal hits certain levels over time. At some set period of time (clock) we are going to "check" the level, and get a value. Then we have some time while the electronics (the line level) will try to settle to its new level and "beat the clock" -- so that when we sample again, things are all in place.
Here is a little timeline chart to help explain how an analog computer (or single signal / line) might work. (This might be similar to something you would see on a logic analyzer or Oscilloscope). The following chart shows four discrete samples (from left to right) with the samples of 3, 2, 3, and 0. And there are basically 4 analog levels.
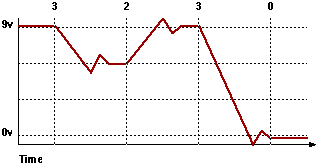
Notice that the red line (the line level) sort of has some "settle" time. It can't just magically jump from one level to another perfectly -- it usually overshoots and then settles in. This means we can't sample until the line has had enough time to get to the point and settle in (stabilize). If we didn't do this we would get a bad value (either too high or too low in voltage) and that would be an error.
We can only sample slower than the worst case transition rate -- the rate it takes to go from maximum to minimum value (or vise versa). During most of the smaller changes (say from a 2 to a 3) the line actually transitions quicker (since it is less far to go), and the line level it is actually ready early and we are just waiting around to sample. This extra delay has to be done, because we don't know if it was a worse case transition until after we sample.
Now lets compare this to what might happen to a digital / binary signal over time.
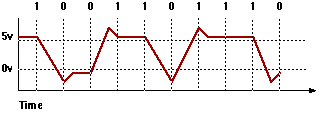
First notice that we don't need as much voltage. There aren't "degrees" or multiple steps in between -- so the electronics can be simpler. We don't need as much voltage, because the resolution (detail) is less -- it is either on or off. Less voltage means that things run cooler (requires less power) -- and the time (distance) to transition from minimum to maximum is decreased as well. So since the level has less distance (time) to travel, things are faster.
Also, unlike analog, the digital signal only has to go beyond a threshold. It doesn't have to be completely "settled in" and be right on -- it can be measured even when it has spiked well past the threshold, with no fear of this giving a false value. Let's face it, it is either on or off. This is a gain, because we don't have to wait for the device to settle (as much) -- and another gain because we can just overpower things (or over drop) and not have to worry about what this will do to the settle time or other levels. This overaction allows us to increase the speed of the transition further.
In our little sample, if we were to go to over 5 volts to 6 volts, we would still get a 1 (on) value. If we were off by that same 20% on the analog sample, we would probably get a false value (reading) and introduce an error. So digital is more reliable (resistant to noise).
In fact, for clarity of signal, you should notice the analog sample only has about 3 volts between the different values. The digital signal has at least 5 volts (and can be a bit more) between levels. So there is a wider spread between values on the digital sample, even though there is less total spread between all values. Again, this means more resistance to noise or errors, and a clearer more discrete signal. And the more levels (samples) you add to the analog, the more susceptible to noise it is.
So by going digital over analog we've increased the speed (more samples in the same amount of time) -- we've decreased the heat, power and simplified the design, and increased the reliability. All of them are wins so far.
The devil is in the details
Of course there are still details -- the biggest issue against digital is that we lost "resolution". The Analog sample had more information (4 levels, either 0, 3 ,6 or 9 volts -- representing a 0,1, 2, or 3), and the binary sample has two level (on or off -- 0 or 1). We can make up for this loss (or less information) in a few different ways.
If you don't understand binary counting, then I recommend you read the article, Binary - Counting Computerese.
One way is by just sending more samples (sequentially or serially). We can just take two samples in a row, and pair them up -- two bits of binary data, give you four possible levels -- which gives us the same detail as our analog sample. (This is basically how a "serial port" sends a stream of bits, and builds them into bytes of data -- but this is getting off topic). Since it takes two digital samples to equal the resolution of one analog one, if you can send the digital sample over twice as fast then you are still ahead. My example only shows the digital as being about 2.5 times faster than the analog one -- but in the real world it is probably more like 8 or 10 times faster or more. And the more resolution in the analog sample, the harder (slower) it can be to get accurate samples.
The other way of sending more digital data, and the way that is use inside computers more often, is by sending lots of samples in parallel (at the same time). Instead of just one binary line, they run many. This offers an even greater performance increase. Look at the following example with 3 lines (bits) of resolution.
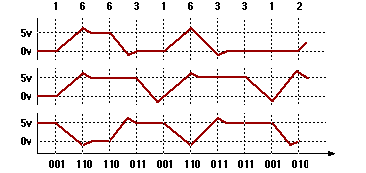
The three bits (lines) at the same time (grouping the signal) gives us 8 possible values (levels) and it doesn't slow down the speed at all. At the top I numbered the decimal "value", and on the bottom I have the binary values (in parallel), but they mean the same thing -- there are 8 combinations from 000 (representing 0) to 111 (representing 7). A table could also help you see the pattern:
0 = 000 2 = 010 4 = 100 6 = 110 1 = 001 3 = 011 5 = 101 7 = 111
No matter how you look at it, our 3 bits (lines) of binary data give us twice the resolution as our analog example -- and we can still take more samples per second. So it is faster, and has more resolution. And I only chose 3 bits (lines). In the 1970s computers used 8 bits at a time (256 levels), and modern computers use 32, 64 or even 128 bits at a time. This is way more resolution than an analog computer could handle on a single line.
On a side note, there are complex issues with sending lots of parallel bits of information over long distances. Basically one line can create interference that bothers the other line, and creates noise (messes with their signal/level). Inside a computer, or a chip, this is easy (easier) to address and control, and most things are done parallel. Outside the computer, on a wire, it is far harder to control, and a lot larger distances, so most problems are solved serial.
Other ways?
The analog example I used was doing something that could be called discrete-analog -- where the analog level is expected to be at an absolute (discrete) value, and not wandering anywhere in between. You could allow a different type of analog, where the signal is some floating level (an infinite-degrees analog), lets call that floating-analog. Floating-analog still has the same issues of settle time and speed, just more resolution crammed in the same space (theoretically an infinite amount). Yet the practicalities of noise and the resolution of the electronics mean that "infinite" is really a not so detailed "finite". In fact, it usually has less levels (in practical terms) than a digital solution could -- this is one of the reasons why things like a CD-player can sound so much better than say an old cassette or AM station. I was also talking about an analog computing device -- computing demands precision and repeatability. This type of floating-analog gets even more errors (is susceptible to noise, environment and gets "slop" in the signal) and all that noise in the signal means that your computing device really becomes an approximation device (as it does not get the same results consistently). So I wouldn't call that an analog computer -- just an analog approximater.
Now some annoyingly inquisitive people might ask, "Are there ways of dealing with bits that are not analog or digital?" The surprising answer is yes. One other way I can think of is called quantum computers and work with something called Qubits (QUantum BITS). These are research projects, and have many issues. I won't even get into it, because it makes my head hurt just thinking about them (let alone trying to explain them), but basically they allow the computer (bit) to be in all states at once (on and off at the same time). Doing mental and logical gymnastics, you are supposed to be able to get the answer you want by knowing exactly what question to ask. Right now they are creating 2 and 4 Qubit machines -- we have a ways to go to get that to levels that will offer practical uses. I think we are still decades away from seeing any practical applications (if ever). Most applications I've heard of have to do with cryptography (cracking) -- but I'm sure there will be more.
If you want to make your brain hurt, just do some research on this subject. Here is a link on the topic. You can also read about Shroedinger's Cat if you like. Einstein was so pissed off by this subject (Quantum Mechanics) that he stated he didn't believe in it and said, "I shall never believe that god plays dice with the universe". Stephen Hawkings retorted, "God not only plays dice with the universe, he sometimes throws them where they cannot be seen."
Conclusion
The only thing constant is change. The way we design and manufacture computers and storage for now makes digital the better solution -- but there is all sorts of research and new concepts being implemented. We have some biological based storage, electrochemical, holographic (light), optical computers, and so on. A major breakthrough in some area might totally change the rules and make analog (multilevel) computing or storage more viable and cost effective again -- so don't rule anything out. I'll just go insane if we start making quantum storage devices and I have to figure out how they work. But for now, and the immediate future, it looks like the world will stay digital -- and I'll retain my tenuous grasp on sanity.
I hope this helps explain to people why computers aren't analog. It isn't that analog is bad, or that it can't be done -- some of the early computers, and some research computers have been analog. It is just that digital is simpler and faster -- which also means cheaper and more reliable. Digital is also very versatile in that you just pair more samples up (add more bits of resolution) to get more detail -- and it can have more detail (discrete levels) than any analog computer (single line) ever could. So we learned through experience that for computers (for now), digital is better.
|